How to Know When You Reject the Null
In our example concerning the hateful class bespeak average, suppose that our random sample of north = xv students majoring in mathematics yields a test statistic t* equaling ii.5. Since n = 15, our test statistic t* has n - one = 14 degrees of freedom. Likewise, suppose we set our significance level α at 0.05, and so that nosotros have simply a 5% gamble of making a Blazon I mistake.
Correct Tailed
The P-value for conducting the right-tailed test H 0 : μ = iii versus H A : μ > 3 is the probability that we would discover a test statistic greater than t* = ii.5 if the population mean \(\mu\) really were 3. Remember that probability equals the expanse under the probability curve. The P-value is therefore the area under a t n - ane = t 14 curve and to the right of the exam statistic t* = 2.v. It tin be shown using statistical software that the P-value is 0.0127. The graph depicts this visually.
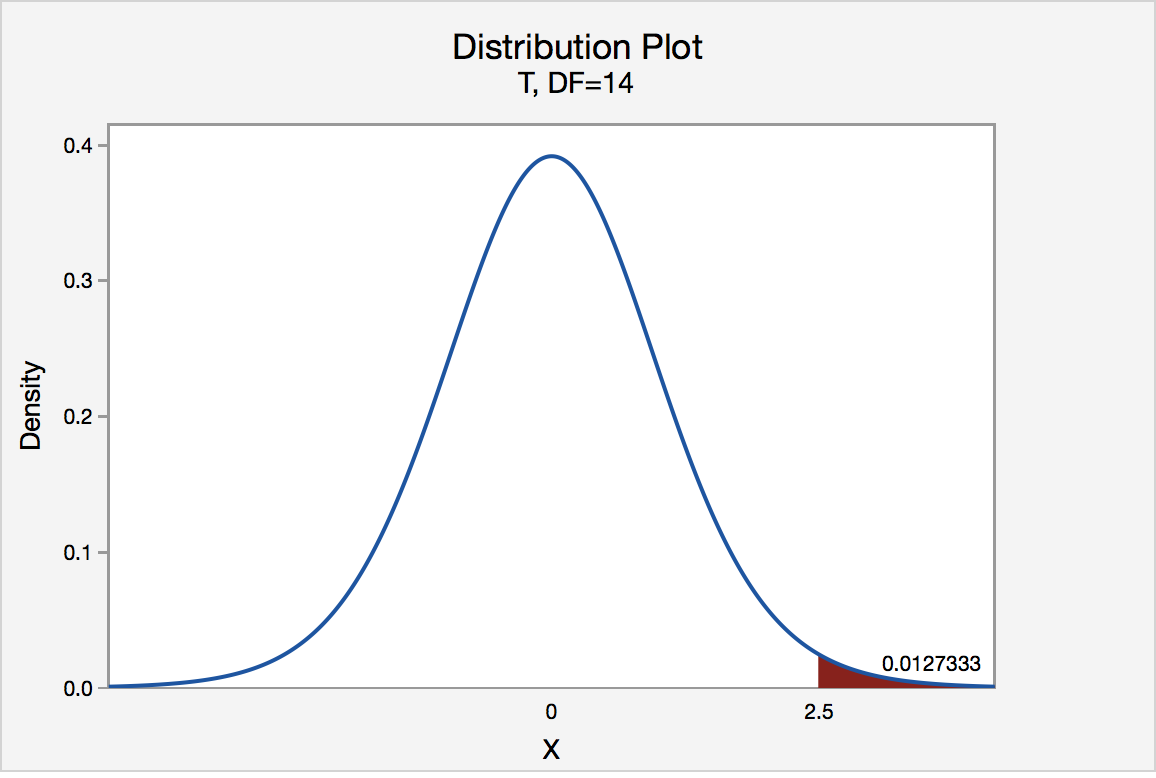
The P-value, 0.0127, tells us information technology is "unlikely" that nosotros would observe such an farthermost examination statistic t* in the direction of H A if the aught hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P-value, 0.0127, is less than \(\alpha\) = 0.05, we reject the goose egg hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > three.
Left Tailed
In our instance concerning the mean grade point boilerplate, suppose that our random sample of n = xv students majoring in mathematics yields a examination statistic t* instead equaling -two.5. The P-value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that nosotros would observe a test statistic less than t* = -2.v if the population mean μ really were three. The P-value is therefore the expanse under a t northward - 1 = t xiv bend and to the left of the test statistic t* = -ii.5. It can be shown using statistical software that the P-value is 0.0127. The graph depicts this visually.
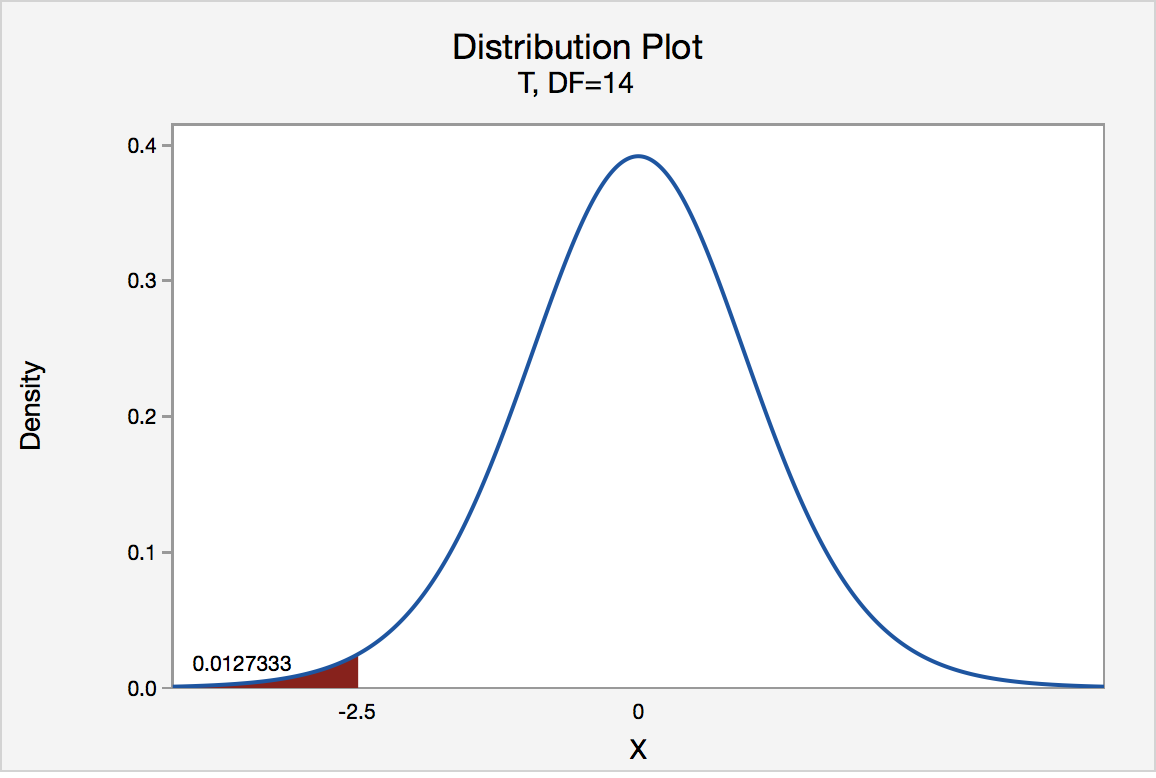
The P-value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P-value, 0.0127, is less than α = 0.05, we reject the zippo hypothesis H 0 : μ = 3 in favor of the culling hypothesis H A : μ < three.
Two Tailed
In our example concerning the mean grade indicate average, suppose over again that our random sample of north = 15 students majoring in mathematics yields a test statistic t* instead equaling -2.5. The P-value for conducting the two-tailed test H 0 : μ = three versus H A : μ ≠ iii is the probability that nosotros would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ actually were 3. That is, the 2-tailed test requires taking into account the possibility that the test statistic could autumn into either tail (and hence the name "two-tailed" exam). The P-value is therefore the surface area nether a t n - 1 = t 14 curve to the left of -2.5 and to the right of the ii.five. It can exist shown using statistical software that the P-value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.
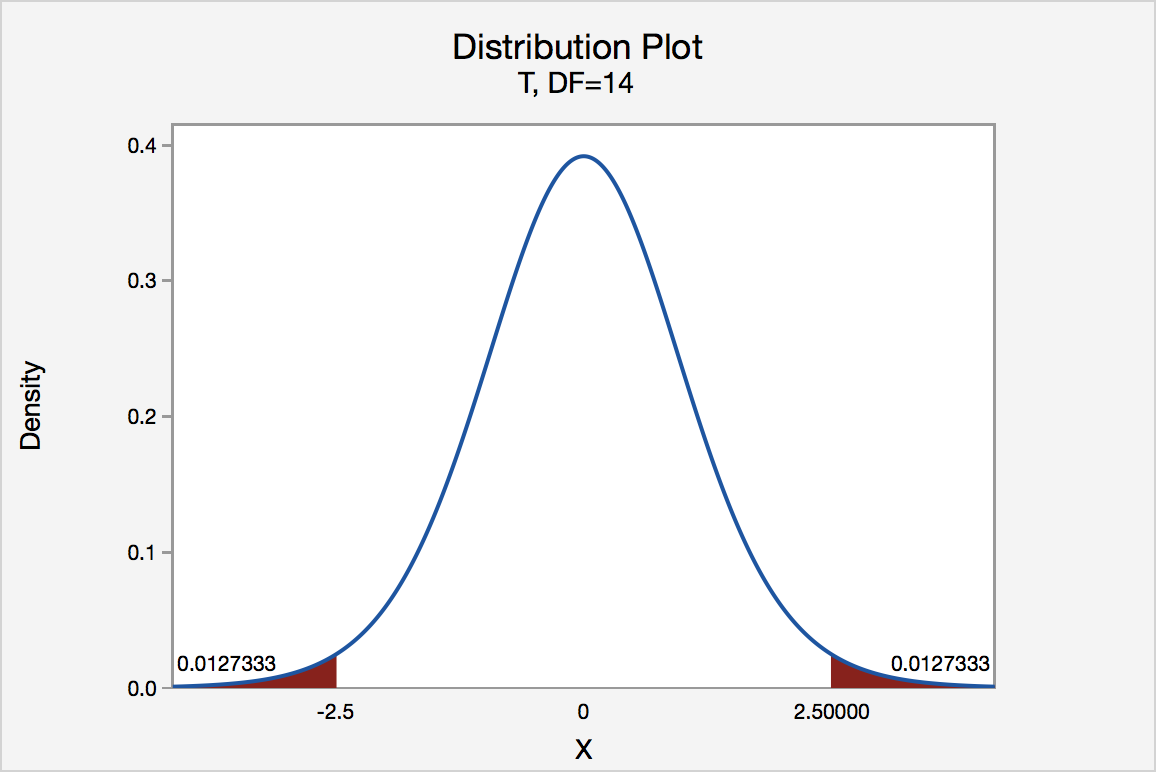
Annotation that the P-value for a two-tailed exam is ever two times the P-value for either of the i-tailed tests. The P-value, 0.0254, tells us it is "unlikely" that we would find such an extreme test statistic t* in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the zip hypothesis is true must exist incorrect. That is, since the P-value, 0.0254, is less than α = 0.05, nosotros reject the null hypothesis H 0 : μ = three in favor of the alternative hypothesis H A : μ ≠ 3.
At present that nosotros take reviewed the disquisitional value and P-value approach procedures for each of three possible hypotheses, let's await at iii new examples — ane of a correct-tailed test, i of a left-tailed exam, and one of a two-tailed test.
The good news is that, whenever possible, we will accept reward of the test statistics and P-values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this grade.
Source: https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing/p-value-approach
0 Response to "How to Know When You Reject the Null"
Post a Comment